Friday, July 20, 2007
Ripple down rules (RDR) is a methodology for creating decision trees, in domains even experts have trouble mapping their knowledge in, by requiring the expert only to justify their correction of the system, in the context in which the particular error occurred. That's probably why the original article on ripple down rules was called Knowledge in context: a strategy for expert system maintenance.
Now, there's two possible approaches to making the RDR system probabilistic (i.e. making it predict the probability that it is wrong for a given input). First, we could try to predict the probabilities based on the structure of the RDR and which rules have fired. Alternatively, we could ask the expert explicitly for some knowledge of probabilities (in the specific context, of course).
Observational analysis
What I'm talking about here is using RDR like normal, but trying to infer probabilities based on the way it reaches its conclusion. The most obvious situation where this will work is when all the rules that conclude positive (interesting) fire and none of the rules that conclude negative (uninteresting) fire. (This does, however, mean creating a more Multiple Classification RDR type of system.) Other possibilities include watching over time to see which rules are more likely to be wrong.
These possibilities may seem week, but they may turn out to provide just enough information. Remember, any indication that some examples are more likely to be useful is good, because it can cut down the pool of potential false negatives from the whole web to something much, much smaller.
An expert opinion
The other possibility is to ask the expert in advance how likely the system is to be wrong. Now, as I discussed, this whole RDR methodology is based around the idea that experts are good at justifying themselves in context, so it doesn't make much sense to ask the expert to look at an RDR system and say in advance how likely a given analysis is to be wrong. On the other hand, it might be possible to ask the expert, when they are creating a new rule: what is the probability that the rule will be wrong (the conclusion is wrong), given that it fires (its condition is met)? And, to get a little bit more rigorous, we would ideally also like to know: what is the probability that the rule's condition will be met, given that the rule's parent fired (the rule's parent's condition was met)?
The obvious problem with this is that the expert might not be able to answer these questions, at least with any useful accuracy. On the other hand, as I said above, any little indication is useful. Also, it's worth pointing out that what we need is not primarily probabilities, but rather a ranking or ordering of the candidates for expert evaluation, so that we know which is the most likely to be useful (rather than exactly how likely it is to be useful).
Also the calculations of probabilities could turn out to be quite complex :)
Here's what I consider a minimal RDR tree for the purposes of calculating probabilities, with some hypothetical (imaginary) given probabilities.
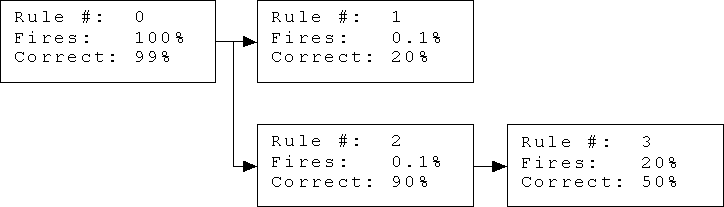
Let me explain. Rule 0 is the default rule (the starting point for all RDR systems). It fires 100% of the time, and in this case it is presumed to be right 99% of the time (simulating the needle-in-a-haystack scenario). Rules 1 and 2 are exceptions to rule 0, and will be considered only when rule 0 fires (which is all the time because it is the default rule). Rule 3 is an exception to rule 2, and will be considered only when rule 2 fires.
The conclusions of rules 0 and 3 are (implicitly) 'hay' (uninteresting), while the conclusions of rules 1 and 2 are (implicitly) 'needle' (interesting). This is because the conclusion of every exception rule needs to be different from the conclusion of the parent rule.
The percentage for 'Fires' represents the expert's opinion of how likely the rule is to fire (have its condition met) given that the rule is reached (its parent is reached and fires). The percentage for 'Correct' represents the expert's opinion of how likely the rule's conclusion is to be correct, given that the rule is reached and fires.
With this setup, you can start to calculate some interesting probabilities, given knowledge of which rules fire for a given example. For example, what is the probability of 'needle' given that rules 1 and 2 both fire, but rule 3 doesn't? (This is assumedly the most positive indication of 'needle' we can get.) What difference would it make if rule 3 did fire? If you can answer either of these questions, leave a comment.
If no rules fire, for example, the probability of 'needle' is 0.89%, which is only very slightly less than the default probability of 'needle' before using the system, which was 1%. Strange, isn't it?
Now, there's two possible approaches to making the RDR system probabilistic (i.e. making it predict the probability that it is wrong for a given input). First, we could try to predict the probabilities based on the structure of the RDR and which rules have fired. Alternatively, we could ask the expert explicitly for some knowledge of probabilities (in the specific context, of course).
Observational analysis
What I'm talking about here is using RDR like normal, but trying to infer probabilities based on the way it reaches its conclusion. The most obvious situation where this will work is when all the rules that conclude positive (interesting) fire and none of the rules that conclude negative (uninteresting) fire. (This does, however, mean creating a more Multiple Classification RDR type of system.) Other possibilities include watching over time to see which rules are more likely to be wrong.
These possibilities may seem week, but they may turn out to provide just enough information. Remember, any indication that some examples are more likely to be useful is good, because it can cut down the pool of potential false negatives from the whole web to something much, much smaller.
An expert opinion
The other possibility is to ask the expert in advance how likely the system is to be wrong. Now, as I discussed, this whole RDR methodology is based around the idea that experts are good at justifying themselves in context, so it doesn't make much sense to ask the expert to look at an RDR system and say in advance how likely a given analysis is to be wrong. On the other hand, it might be possible to ask the expert, when they are creating a new rule: what is the probability that the rule will be wrong (the conclusion is wrong), given that it fires (its condition is met)? And, to get a little bit more rigorous, we would ideally also like to know: what is the probability that the rule's condition will be met, given that the rule's parent fired (the rule's parent's condition was met)?
The obvious problem with this is that the expert might not be able to answer these questions, at least with any useful accuracy. On the other hand, as I said above, any little indication is useful. Also, it's worth pointing out that what we need is not primarily probabilities, but rather a ranking or ordering of the candidates for expert evaluation, so that we know which is the most likely to be useful (rather than exactly how likely it is to be useful).
Also the calculations of probabilities could turn out to be quite complex :)
Here's what I consider a minimal RDR tree for the purposes of calculating probabilities, with some hypothetical (imaginary) given probabilities.

Let me explain. Rule 0 is the default rule (the starting point for all RDR systems). It fires 100% of the time, and in this case it is presumed to be right 99% of the time (simulating the needle-in-a-haystack scenario). Rules 1 and 2 are exceptions to rule 0, and will be considered only when rule 0 fires (which is all the time because it is the default rule). Rule 3 is an exception to rule 2, and will be considered only when rule 2 fires.
The conclusions of rules 0 and 3 are (implicitly) 'hay' (uninteresting), while the conclusions of rules 1 and 2 are (implicitly) 'needle' (interesting). This is because the conclusion of every exception rule needs to be different from the conclusion of the parent rule.
The percentage for 'Fires' represents the expert's opinion of how likely the rule is to fire (have its condition met) given that the rule is reached (its parent is reached and fires). The percentage for 'Correct' represents the expert's opinion of how likely the rule's conclusion is to be correct, given that the rule is reached and fires.
With this setup, you can start to calculate some interesting probabilities, given knowledge of which rules fire for a given example. For example, what is the probability of 'needle' given that rules 1 and 2 both fire, but rule 3 doesn't? (This is assumedly the most positive indication of 'needle' we can get.) What difference would it make if rule 3 did fire? If you can answer either of these questions, leave a comment.
If no rules fire, for example, the probability of 'needle' is 0.89%, which is only very slightly less than the default probability of 'needle' before using the system, which was 1%. Strange, isn't it?
Labels: artificial intelligence, ben, research

